Introduction to Logarithms

In its simplest grade, a logarithm answers the question:

How many of one number do we multiply to get another number?

Example: How many 2s do we multiply to get 8?

Reply: two × two × 2 = 8, and then we had to multiply 3 of the iisouth to get 8

So the logarithm is 3

How to Write information technology

We write "the number of 2s we demand to multiply to become 8 is 3" as:

logtwo(viii) = 3

And so these ii things are the aforementioned:

logarithm concept 2x2x2=8 same as log_2(8)=3

The number we multiply is called the "base", then we can say:

  • "the logarithm of 8 with base of operations 2 is three"
  • or "log base two of 8 is 3"
  • or "the base-2 log of 8 is three"

Observe we are dealing with 3 numbers:

  • the base: the number we are multiplying (a "2" in the example above)
  • how ofttimes to use it in a multiplication (three times, which is the logarithm)
  • The number we want to go (an "viii")

More than Examples

Example: What is log5(625) ... ?

Nosotros are request "how many 5s need to be multiplied together to go 625?"

5 × 5 × 5 × 5 = 625, and then nosotros need 4 of the 5s

Reply: logfive(625) = 4

Example: What is log2(64) ... ?

We are asking "how many 2s need to be multiplied together to go 64?"

2 × 2 × 2 × 2 × 2 × 2 = 64, so we need half dozen of the 2s

Respond: log2(64) = 6

Exponents

Exponents and Logarithms are related, let's find out how ...

2 cubed

The exponent says how many times to use the number in a multiplication.

In this example: ii3 = 2 × two × 2 = 8

(ii is used 3 times in a multiplication to get 8)

So a logarithm answers a question like this:

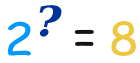
2 with what exponent = 8

In this fashion:

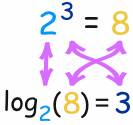
2^3=8 becomes log_2(8)=3

The logarithm tells us what the exponent is!

In that example the "base" is ii and the "exponent" is 3:

2^3=8 becomes log_2(8)=3

So the logarithm answers the question:

What exponent do we demand
(for one number to become another number) ?

The general example is:

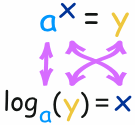
a^x=y becomes log_a(y)=x

Example: What is logten(100) ... ?

102 = 100

So an exponent of 2 is needed to make 10 into 100, and:

logten(100) = 2

Example: What is logthree(81) ... ?

three4 = 81

And so an exponent of iv is needed to make three into 81, and:

logthree(81) = 4

Common Logarithms: Base of operations x

Sometimes a logarithm is written without a base of operations, similar this:

log(100)

This commonly means that the base of operations is actually 10.

log

It is chosen a "common logarithm". Engineers love to employ it.

On a figurer it is the "log" push button.

Information technology is how many times we need to use x in a multiplication, to become our desired number.

Example: log(one thousand) = log10(1000) = 3

Natural Logarithms: Base "due east"

Some other base of operations that is often used is e (Euler's Number) which is near two.71828.

calculator ln button

This is called a "natural logarithm". Mathematicians utilize this i a lot.

On a calculator it is the "ln" push.

It is how many times nosotros demand to employ "due east" in a multiplication, to get our desired number.

Example: ln(7.389) = loge(7.389) ≈ 2

Because ii.718282 ≈ vii.389


But Sometimes In that location Is Confusion ... !

Mathematicians use "log" (instead of "ln") to mean the natural logarithm. This tin lead to confusion:

Example Engineer
Thinks		 Mathematician
Thinks
log(50) logten(50) loge(50) confusion
ln(50) loge(50) loge(50) no confusion
logx(l) log10(50) logten(l) no defoliation

And so, exist careful when you read "log" that you know what base they mean!

Logarithms Can Have Decimals

All of our examples have used whole number logarithms (like ii or 3), but logarithms can have decimal values like ii.5, or half dozen.081, etc.

Instance: what is log10(26) ... ?

log

Get your calculator, type in 26 and press log

Respond is: one.41497...

The logarithm is saying that x1.41497... = 26
(10 with an exponent of ane.41497... equals 26)

This is what it looks like on a graph:

See how overnice and smooth the line is.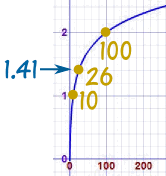

 log 10 of 26

Read Logarithms Can Take Decimals to notice out more.

Negative Logarithms

− Negative? But logarithms deal with multiplying.
What is the reverse of multiplying? Dividing!

A negative logarithm means how many times to divide past the number.

We tin accept just 1 split:

Example: What is logviii(0.125) ... ?

Well, one ÷ eight = 0.125,

So log8(0.125) = −1

Or many divides:

Case: What is logv(0.008) ... ?

1 ÷ 5 ÷ 5 ÷ v = 5−3 ,

So logfive(0.008) = −3

It All Makes Sense

Multiplying and Dividing are all part of the aforementioned elementary pattern.

Let usa look at some Base of operations-10 logarithms equally an example:

Number How Many 10s Base-10 Logarithm
10 times larger / smaller .. etc..
chiliad 1 × x × 10 × ten log10(thou) = 3
100 1 × x × 10 logten(100) = 2
10 1 × 10 logx(10) = i
1 1 log10(ane) = 0
0.one one ÷ x logten(0.1) = −1
0.01 1 ÷ 10 ÷ ten log10(0.01) = −ii
0.001 one ÷ x ÷ 10 ÷ 10 log10(0.001) = −3
.. etc..

Looking at that table, run across how positive, zero or negative logarithms are really part of the aforementioned (fairly simple) pattern.

The Word

"Logarithm" is a word made up by Scottish mathematician John Napier (1550-1617), from the Greek discussion logos significant "proportion, ratio or word" and arithmos meaning "number", ... which together makes "ratio-number" !